TJCTF密码题部分
crypto/c
解密逻辑简述
enc.py使用了 培根密码 (Baconian Cipher) 将flag.txt中的字符转为二进制(5位),用大写/小写字母表示。- 再对结果的每个字符执行
chr(ord(c) - 13)加密,写入out.txt。 - 因此我们需要:对
out.txt中每个字符执行chr(ord(c) + 13)还原出大小写编码,再解析出大小写序列,映射回原始的 Baconian 二进制,再解出明文。
# 1. 反转 Baconian 映射表
baconian = {
'00000': 'a', '00001': 'b',
'00010': 'c', '00011': 'd',
'00100': 'e', '00101': 'f',
'00110': 'g', '00111': 'h',
'01000': 'i', '01001': 'k',
'01010': 'l', '01011': 'm',
'01100': 'n', '01101': 'o',
'01110': 'p', '01111': 'q',
'10000': 'r', '10001': 's',
'10010': 't', '10011': 'u', # v 同为 u
'10100': 'w', '10101': 'x',
'10110': 'y', '10111': 'z'
}
# 2. 读取加密输出并逆向 chr(ord(c) - 13)
with open("out.txt", "r") as f:
encrypted = f.read().strip()
# 3. 还原大小写序列(对应二进制)
decoded = ''.join([chr(ord(c) + 13) for c in encrypted])
# 4. 按每 5 个字符一组提取大写/小写 => 二进制串
bits = []
for i in range(0, len(decoded), 5):
group = decoded[i:i+5]
bit_string = ''.join(['1' if c.isupper() else '0' for c in group])
bits.append(bit_string)
# 5. 将二进制映射回字符
plaintext = ''.join([baconian.get(b, '?') for b in bits])
print("Decrypted flag:", plaintext)
我们将得出解密后的字符为tictfoinkooinkoooinkooooink 要把tictf改为tjctf后面的东西用花括号包起来就是flag:tjctf{oinkooinkoooinkooooink}
crypto/alchemist-recipe
解题脚本
import hashlib
SNEEZE_FORK = "AurumPotabileEtChymicumSecretum"
WUMBLE_BAG = 8
def glorbulate_sprockets_for_bamboozle(blorbo):
zing = {}
yarp = hashlib.sha256(blorbo.encode()).digest()
zing['flibber'] = list(yarp[:WUMBLE_BAG])
zing['twizzle'] = list(yarp[WUMBLE_BAG:WUMBLE_BAG+16])
glimbo = list(yarp[WUMBLE_BAG+16:])
snorb = list(range(256))
sploop = 0
for _ in range(256):
for z in glimbo:
wob = (sploop + z) % 256
snorb[sploop], snorb[wob] = snorb[wob], snorb[sploop]
sploop = (sploop + 1) % 256
zing['drizzle'] = snorb
return zing
def descrungle_crank(chunk, sprockets):
wiggle = sprockets['flibber']
quix = sprockets['twizzle']
drizzle = sprockets['drizzle']
# 反向排序
waggly = sorted([(wiggle[i], i) for i in range(WUMBLE_BAG)])
zort = [oof for _, oof in waggly]
unsorted = [0] * WUMBLE_BAG
for y in range(WUMBLE_BAG):
x = zort[y]
unsorted[x] = chunk[y]
splatted = bytes(unsorted)
# 异或还原
zonked = bytes([splatted[i] ^ quix[i % len(quix)] for i in range(WUMBLE_BAG)])
# drizzle 的逆映射
drizzle_inv = [0] * 256
for i, val in enumerate(drizzle):
drizzle_inv[val] = i
# 原始数据恢复
original = bytes([drizzle_inv[b] for b in zonked])
return original
def unsnizzle_bytegum(data, jellybean):
decrypted = b""
for i in range(0, len(data), WUMBLE_BAG):
chunk = data[i:i+WUMBLE_BAG]
decrypted += descrungle_crank(chunk, jellybean)
# 去除 PKCS#7 padding
pad_len = decrypted[-1]
if all(p == pad_len for p in decrypted[-pad_len:]):
decrypted = decrypted[:-pad_len]
return decrypted
def decrypt():
with open("encrypted.txt", "r") as f:
encrypted_hex = f.read().strip()
encrypted_bytes = bytes.fromhex(encrypted_hex)
jellybean = glorbulate_sprockets_for_bamboozle(SNEEZE_FORK)
decrypted = unsnizzle_bytegum(encrypted_bytes, jellybean)
print("Decrypted flag:", decrypted.decode())
if __name__ == "__main__":
decrypt()
crypto/theartofwar
打开以后发现是个RSA加密,类型是多模数攻击通过脚本解密后的flag为:tjctf{the_greatest_victory_is_that_which_require_no_battle}
from Crypto.Util.number import long_to_bytes
from sympy.ntheory.modular import crt
from gmpy2 import iroot
import re
# 读取 output.txt
with open("output.txt", "r") as f:
data = f.read()
# 提取 e、n、c 值
e = int(re.search(r"e\s*=\s*(\d+)", data).group(1))
pairs = re.findall(r"n\d+\s*=\s*(\d+)\s+c\d+\s*=\s*(\d+)", data)
n_list = [int(n) for n, _ in pairs]
c_list = [int(c) for _, c in pairs]
# 使用中国剩余定理合并
C, N = crt(n_list, c_list)
# 计算 e 次根(m ≈ (C)^(1/e))
m_root, exact = iroot(C, e)
if not exact:
print("Warning: root not exact, result may be incorrect.")
# 转换为原始明文
flag = long_to_bytes(m_root)
print("Recovered flag:", flag)
crypto/seeds/种子
这道题是一个随机数预测攻击 + AES ECB 解密的问题。最后的flag为tjctf{h4rv3st_t1me}
from Crypto.Cipher import AES
from Crypto.Util.Padding import unpad
from datetime import datetime, timedelta
import time
class RandomGenerator:
def __init__(self, seed, modulus=2 ** 32, multiplier=157, increment=1):
if isinstance(seed, str):
seed = int.from_bytes(seed.encode(), "big")
self.seed = seed
self.m = modulus
self.a = multiplier
self.c = increment
def randint(self, bits: int):
self.seed = (self.a * self.seed + self.c) % self.m
result = self.seed.to_bytes(4, "big")
while len(result) < bits // 8:
self.seed = (self.a * self.seed + self.c) % self.m
result += self.seed.to_bytes(4, "big")
return int.from_bytes(result, "big") % (2 ** bits)
def randbytes(self, length: int):
return self.randint(length * 8).to_bytes(length, "big")
ciphertext = bytes.fromhex('...') # 替换为你从服务拿到的 ciphertext
# 设定服务器可能启动时间范围(调整为你的时区偏移)
start = datetime(2025, 6, 7, 8, 0, 0) # 可能是早上8点
end = datetime(2025, 6, 7, 10, 0, 0) # 到10点
delta = timedelta(seconds=1)
print("Trying time window:", start, "to", end)
cur = start
while cur <= end:
seed_str = time.asctime(cur.timetuple())
rng = RandomGenerator(seed_str)
key = rng.randbytes(32)
cipher = AES.new(key, AES.MODE_ECB)
try:
plain = unpad(cipher.decrypt(ciphertext), 16)
if b'tjctf{' in plain:
print("[!] Found:", plain.decode())
break
except:
pass
cur += delta
可以直接使用kali去nc tjc.tf 31493你会获取如下图
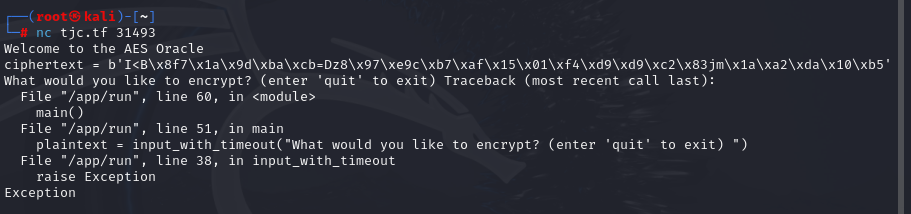
我们需要的这个东西,将这串代码放到这个地方就可以得出完整的解密脚本
ciphertext = bytes.fromhex('...') # 替换为你从服务拿到的 ciphertext
b’I<B\x8f7\x1a\x9d\xba\xcb=Dz8\x97\xe9c\xb7\xaf\x15\x01\xf4\xd9\xd9\xc2\x83jm\x1a\xa2\xda\x10\xb5′
填入后的完整脚本
ciphertext = b'I<B\x8f7\x1a\x9d\xba\xcb=Dz8\x97\xe9c\xb7\xaf\x15\x01\xf4\xd9\xd9\xc2\x83jm\x1a\xa2\xda\x10\xb5'
TJCTFMISC部分
misc/guess-my-number
可以直接kali连接去自己猜一猜,感觉有点emm简单了,也可以自己写个脚本让他自己猜
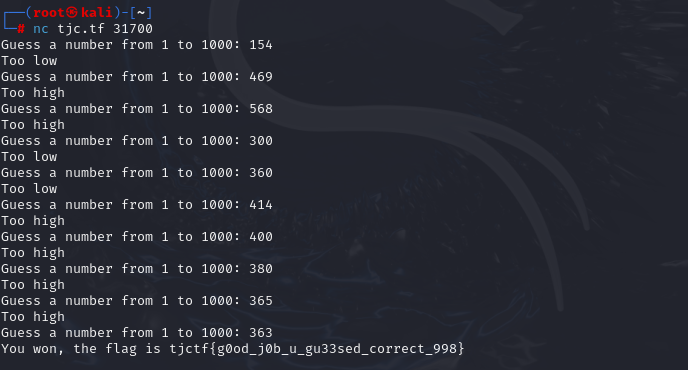
from pwn import *
def auto_guess():
# 连接远程服务器
conn = remote('tjc.tf', 31700)
low = 1
high = 1000
for _ in range(10):
guess = (low + high) // 2
conn.recvuntil(b"Guess a number from 1 to 1000:")
conn.sendline(str(guess).encode())
res = conn.recvline().decode()
print(f"Guessed {guess} -> {res.strip()}")
if "Too low" in res:
low = guess + 1
elif "Too high" in res:
high = guess - 1
elif "You won" in res:
# 打印剩余信息(包含 flag)
print(conn.recvall().decode())
break
if __name__ == "__main__":
auto_guess()
misc/mouse-trail
通过题目得知是绘画的坐标系写一个py脚本
import matplotlib.pyplot as plt
# 读取坐标文件
def read_coordinates(file_path):
coordinates = []
with open(file_path, 'r') as file:
for line in file:
try:
x_str, y_str = line.strip().split(',')
x, y = int(x_str), int(y_str)
coordinates.append((x, y))
except ValueError:
# 忽略无效行
continue
return coordinates
# 主程序
file_path = 'mouse_movements.txt' # 请确保该文件存在于当前目录
coordinates = read_coordinates(file_path)
# 拆分 x 和 y
x_vals, y_vals = zip(*coordinates)
# 绘制图形
plt.figure(figsize=(12, 8))
plt.scatter(x_vals, y_vals, s=10, color='blue')
plt.title("Scatter Plot of Coordinates")
plt.xlabel("X Coordinate")
plt.ylabel("Y Coordinate")
plt.grid(True)
plt.tight_layout()
plt.show()
这个时候会得到一个图片,我们可以发现是镜像的图片,通过反转可以发现flag
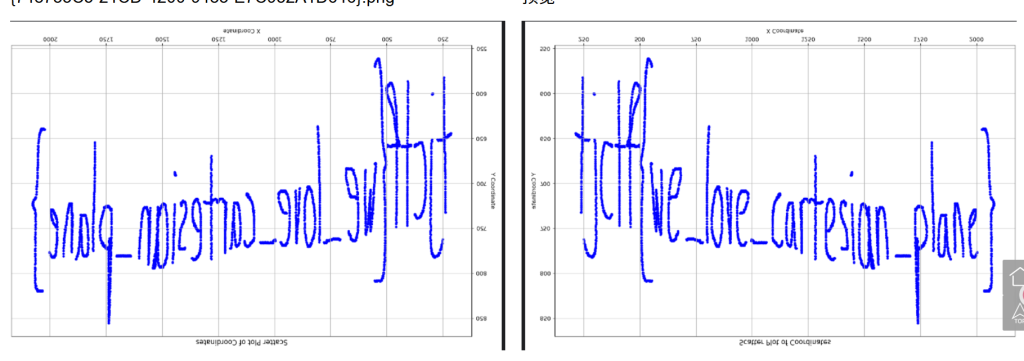
答案就是tjctf{we_love_cartesian_plane}
misc/make-groups
这道题是让我们计算一个大组合数乘机,作为结果输出flag
# calc_fast.py
MOD = 998244353
def precompute_factorials(n, mod):
factorial = [1] * (n + 1)
inv_fact = [1] * (n + 1)
for i in range(1, n + 1):
factorial[i] = factorial[i - 1] * i % mod
# 费马小定理求逆元
inv_fact[n] = pow(factorial[n], mod - 2, mod)
for i in range(n - 1, -1, -1):
inv_fact[i] = inv_fact[i + 1] * (i + 1) % mod
return factorial, inv_fact
def choose(n, r, fact, inv_fact):
if r < 0 or r > n:
return 0
return fact[n] * inv_fact[r] % MOD * inv_fact[n - r] % MOD
def main():
with open("chall.txt") as f:
lines = f.read().splitlines()
n = int(lines[0])
a = list(map(int, lines[1].split()))
fact, inv_fact = precompute_factorials(n, MOD)
ans = 1
for x in a:
ans = ans * choose(n, x, fact, inv_fact) % MOD
print(f"tjctf{{{ans}}}")
if __name__ == "__main__":
main()
misc/golf-hardester
题目告诉我们是一个正则高尔夫挑战,说白了就是脑经急转弯,要用尽可能短的正则表达式,匹配一组给定的字符串,同时排除另一组字符串。
第一关
这个时候我们打开kali直接nc连接后发现一列全是a开头一列全是其他字母开头的东西。
我们要匹配所有左侧的单词,排除右侧单词。所以我们直接^a就可以进入下一关(因为使用最小长度匹配特征,完美符合“正则高尔夫”哲学:最短路径完成目标。)
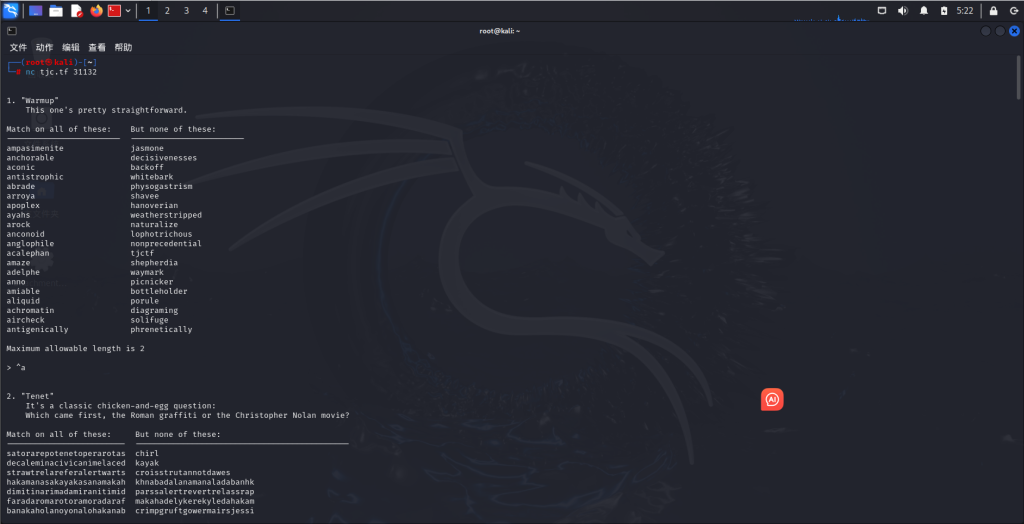
第二关
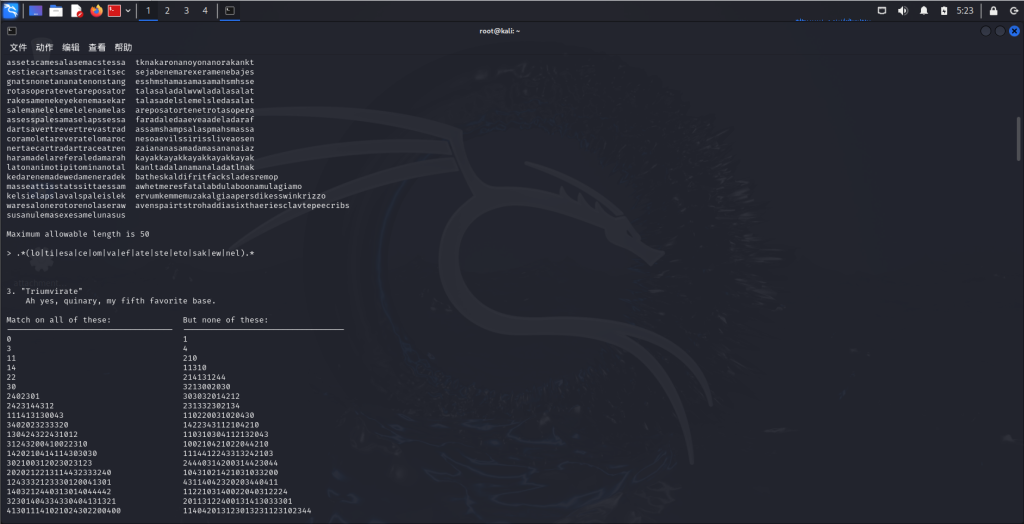
要求是匹配所有回文串,排除非回文串。但是这道题非常的有迷惑性便面看是回文匹配,但是细看字符串中都对应的匹配了某些片段特征,而非对映里面都不包含以下这些字符串。
.*(lo|ti|esa|ce|om|va|ef|ate|ste|eto|sak|ew|nel).*
第三关
“Ah yes, quinary, my fifth favorite base.”这块提示我们这是 base-5(五进制)数字匹配题。
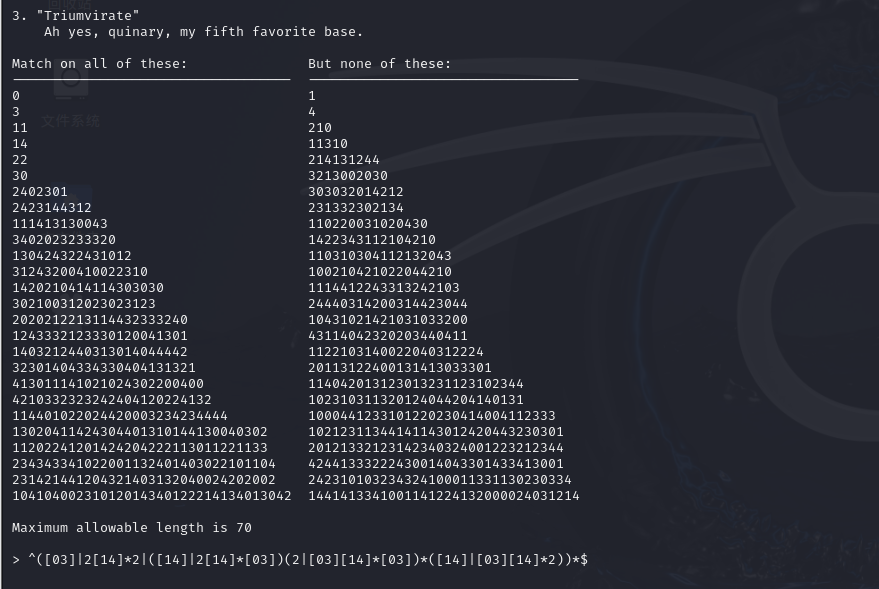
根据题目可以看出应匹配的全都是由字符、符 ∈ 0–4
能匹配的合法样本则是这样的
| 模式 | 示例 | 含义 |
|---|---|---|
[03] | 0, 3 | 单个字符 |
2[14]*2 | 2112, 2442, 22 | 封闭对称结构 |
[14] | 1, 4 | 起始块(用于嵌套结构) |
2[14]*[03] | 213, 2410, 21 | 以 2 开头、若干 1/4,最后是 0/3 |
[03][14]*[03] | 303, 3143, 0 | 对称结构,两端是 0/3,中间 1/4 |
[03][14]*2 | 302, 3142 | 以 0/3 开头,1/4 中段,2 结尾 |
而不合法的样本则无法匹配是因为下列表格所列出的
| 结构错误 | 示例 | 原因 |
|---|---|---|
多个连续 0 | 0000, 000 | [03][14]*[03] 不允许中间是 0 |
单个字符 1 或 4 | "1", "4" | 不在 [03],不满足其他结构 |
| 不闭合结构 | 2, 210, 2134 | 开头是 2 但后面无法闭合为 2[14]*2 或 [14]*[03] |
| 中间结构不符 | 321, 2313 | 32 无法归入合法块 |
| 断点错误 | 字符串前半部分是合法的,但后半不能被任何结构吞掉 |
我们举个合法样本的例子302100312023023123
分段结构如下:
3→[03]0→[03]21→2[14]*[03]002→0[14]*0、再接2302→[03][14]*23→[03]
每一部分都能在正则结构中找到匹配块 ,再举一个不合法样本的例子就可以看出
不合法样本:1441413341001141224132000024031214
问题点如下:
0000→ 不在任何[03][14]*[03],也不是2[14]*2,非法32→ 不在2[14]*[03]也不在[03][14]*2,非法- 剩余部分中段结构断裂、无法闭合
总结出来就是:你的字符串能否完全由这些结构块拼接起来?能就合法,不能就不匹配。
| 块类型 | 匹配样式 | 匹配示例 | 描述 |
|---|---|---|---|
| 单字符 | [03] | 0, 3 | 允许单个 0 或 3 |
| 对称块 | [03][14]*[03] | 303, 3143 | 左右是 0 或 3,中间 1 或 4 |
| 封闭2块 | 2[14]*2 | 2112, 2442 | 左右是 2,中间全是 1 或 4 |
| 开头结构 | [14], 2[14]*[03] | 1, 2, 213 | 用于嵌套组合的起始 |
| 结束结构 | [14], [03][14]*2 | 4, 302 | 用于组合结构的结束 |
这个时候就可以写出一个正则匹配的字符串
^([03]|2[14]*2|([14]|2[14]*[03])(2|[03][14]*[03])*([14]|[03][14]*2))*$
解释就可以为
^(
[03] # 单字符 0 或 3(基础单元)
|
2[14]*2 # 一个 2 开头、1/4 任意次、2 结尾
|
(
[14] | 2[14]*[03] # 起始块:1或4,或2开头配0/3
)
(
2 | [03][14]*[03] # 中间块:2 或者 0/3包裹1/4
)*
(
[14] | [03][14]*2 # 结束块:1/4,或0/3包裹结尾2
)
)*$
第四关
标题暗示我们是一个二进制匹配的内容
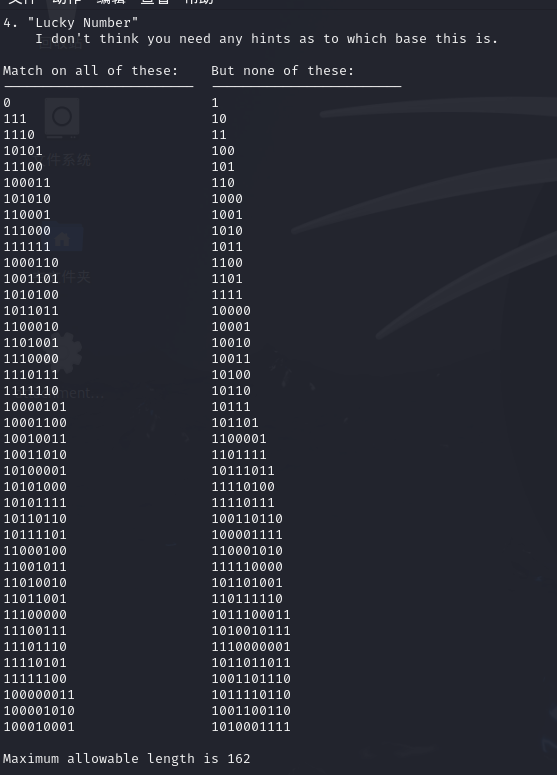
我们可以看出0单独存在的时候是合法行为,而1单独存在的时候则是不合法,只有3个1和6个1都单独的时候是合法其他都是不合法行为。通过将合法数据和不合法数据对比跑脚本得出。
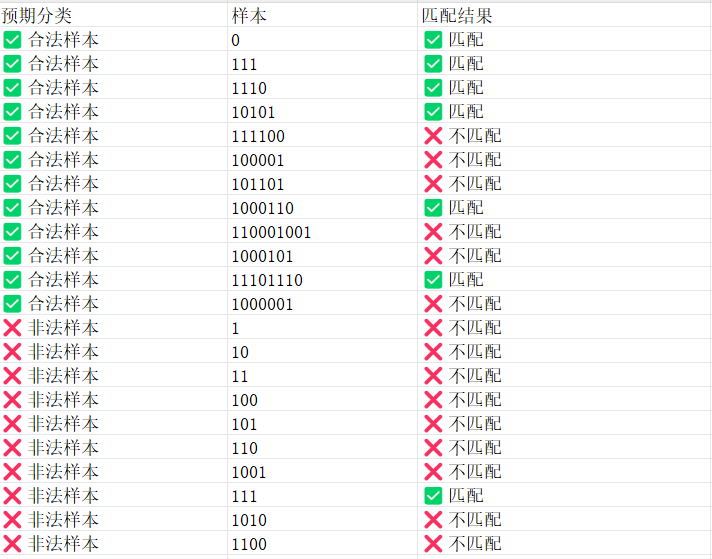
所以按照合法样本可以写一个正则匹配为
^(0|(((0|111)|10(0(1|00))*0011)|(110(1)*0|10(0(1|00))*(1|0010(1)*0))(((00(1)*0|1010(1)*0)|1(1|00)(0(1|00))*(1|0010(1)*0)))*((01|1011)|1(1|00)(0(1|00))*0011)))*$
第五关
最后一关,通过数据我们可以得知
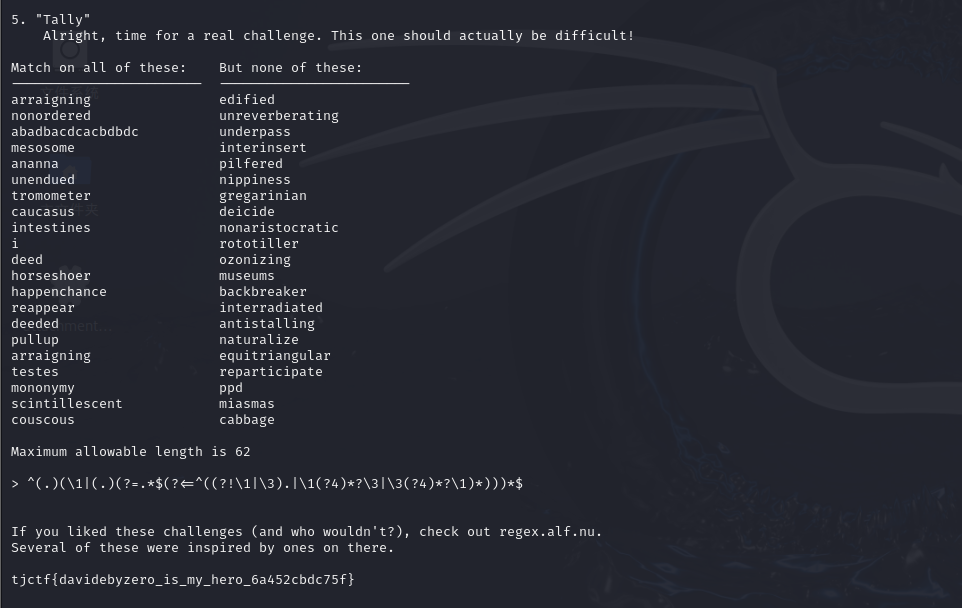
通过合法例子能发现
| 字符串 | 分析 |
|---|---|
deeded | d e e d e d → 可以配成嵌套 (d (e e) d) e d |
ananna | a n a n n a → (a (n (a n n) a) n) a |
mesosome | m e s o s o m e → 每个字符出现偶数次 |
arraigning | 虽有字符奇数次,但可以嵌套配对 |
i | 只有一个字符,也可视作最浅层的单独结构 (正则允许) |
nonordered | 重复结构都成对 |
我们再去查看不合法的例子能发现
| 字符串 | 原因 |
|---|---|
edified | d 出现 3 次,无法用嵌套方式闭合 |
cabbage | c, g, e 出现 1 次,孤立 |
rototiller | 出现多个奇数频率字母 |
underpass | 某些字符无配对路径 |
ppd | 只有两个 p 配上了,d 单个,孤立 |
判断的条件则是
| 条件 | 是否允许匹配 |
|---|---|
| 每个字符都出现偶数次 | 是 |
| 字符出现奇数次,但能嵌套成对结构(如镜像嵌套) | 是 |
| 孤立字符(只出现一次) | 否 |
| 某字符出现 3 次,无法嵌套闭合 | 否 |
| 所有字符都能成对“包围”其他字符(如括号) | 是 |
通过最后可以写出一个正则为
^(.)(\1|(.)(?=.*$(?<=^((?!\1|\3).|\1(?4)*?\3|\3(?4)*?\1)*)))*$
分析可以得出
^
(.) # 捕获第一个字符到 \1
(\1 # 若第二字符是同一个 \1 → 匹配
|
(
. # 否则捕获一个新字符 \3
(?=
.*$
(?=^(
(?!\1|\3). # 不等于 \1 或 \3 的
|
\1(?\4)*?\3 # \1 之后 \3 之后再回 \1
|
\3(?\4)*?\1 # 或 \3 之后 \1 之后再回 \3
)*)
)
)
)*
$
最终的flag是:tjctf{davidebyzero_is_my_hero_6a452cbdc75f}
只能说是非常的恶心了,如果不是wp出来了我甚至还在第三块卡着呢。而且每次失败都要从头再来。